Polarized observations¶
This tutorial covers working with polarized instrument and maps, and recovering polarized maps from observations.
We start with a normal instrument, and create two orthogonally polarized copies of each detector by setting polarized: True in the Array config:
[1]:
import maria
from maria.instrument import Band
f090 = Band(
center=90e9, # in Hz
width=20e9, # in Hz
NET_RJ=40e-6, # in K sqrt(s)
knee=1e0, # in Hz
gain_error=5e-2)
f150 = Band(
center=150e9,
width=30e9,
NET_RJ=60e-6,
knee=1e0,
gain_error=5e-2)
array = {"field_of_view": 0.5,
"shape": "circle",
"beam_spacing": 1.5,
"primary_size": 10,
"polarized": True,
"bands": [f090, f150]}
instrument = maria.get_instrument(array=array)
print(instrument.arrays)
n FOV baseline bands polarized
array1 652 28.68’ 0 m [f090,f150] True
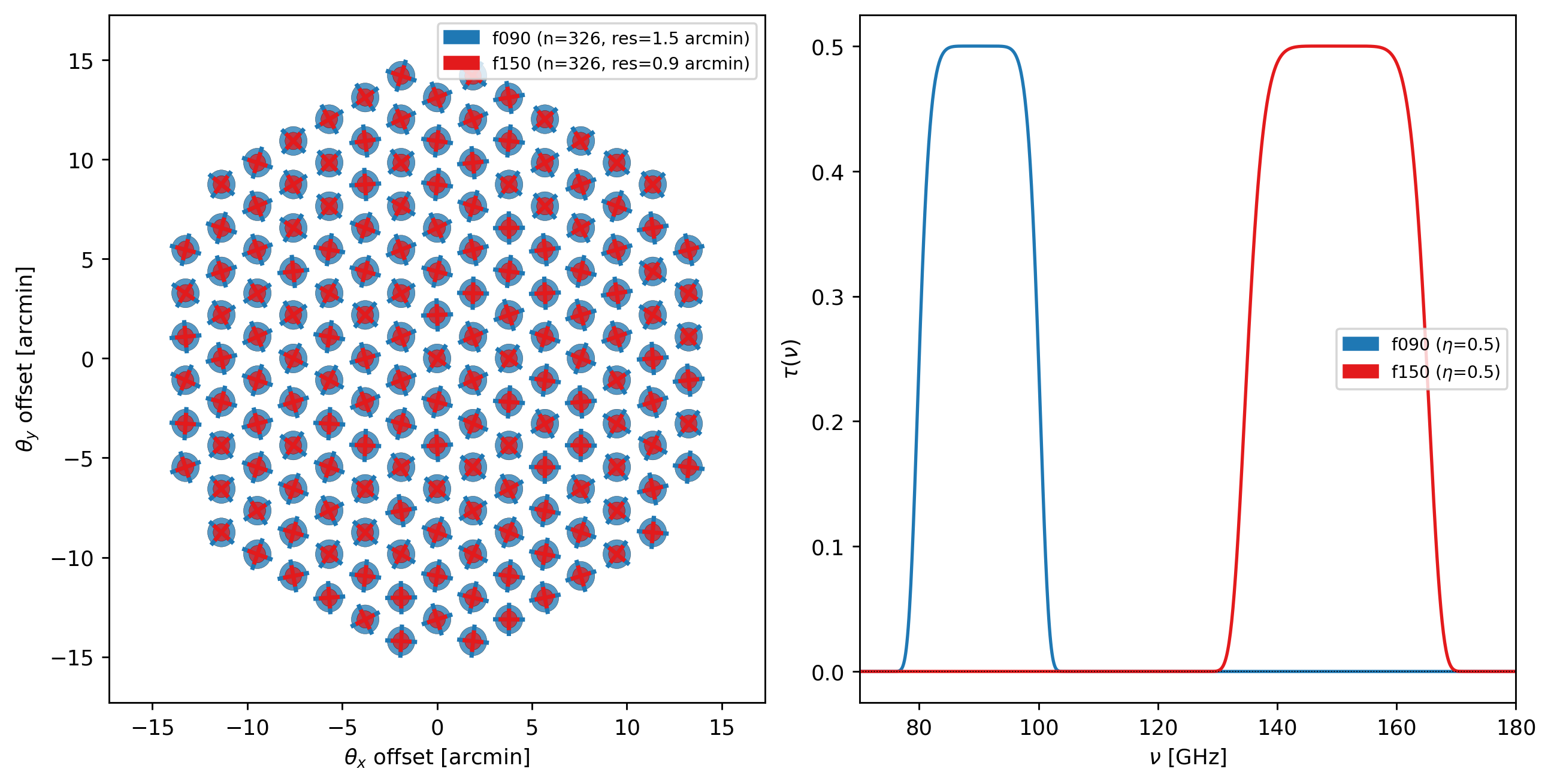
We can see the resulting polarization footprint in the instrument plot:
[2]:
print(instrument)
instrument.plot()
Instrument(1 array)
├ arrays:
│ n FOV baseline bands polarized
│ array1 652 28.68’ 0 m [f090,f150] True
│
└ bands:
name center width η NEP NET_RJ NET_CMB FWHM
0 f090 90 GHz 20 GHz 0.5 5.445 aW√s 40 uK√s 49.13 uK√s 1.458’
1 f150 150 GHz 30 GHz 0.5 12.25 aW√s 60 uK√s 104 uK√s 0.8748’
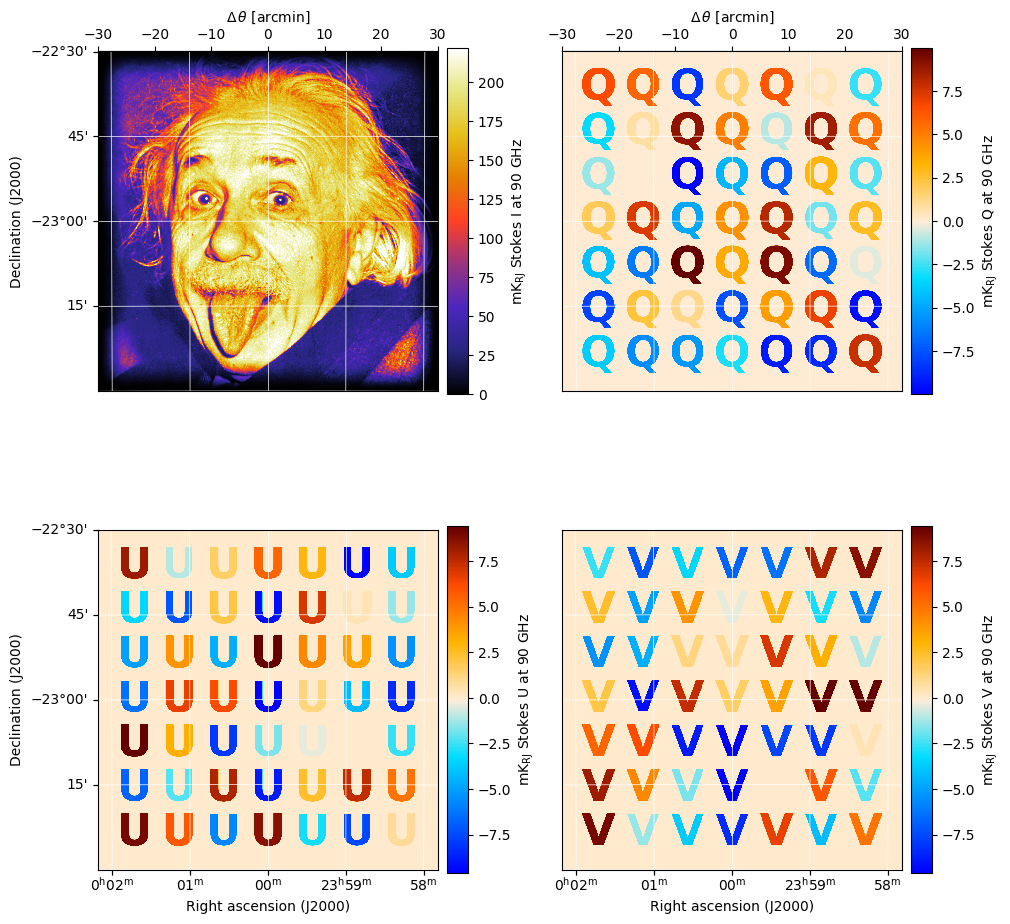
Let’s observe the use the Einstein map, which has a faint polarization signature underneath the unpolarized signal of Einstein’s face. Remember that all maps are five dimensional (stokes, frequency, time, y, x); this map has four channels in the stokes dimensions (the I, Q, U, and V Stokes parameters). We can plot all the channels by giving plot a shaped set of stokes parameters.
[3]:
from maria.io import fetch
input_map = maria.map.load(fetch("maps/einstein.h5"))
input_map.plot(stokes=[["I", "Q"],
["U", "V"]])
Downloading https://github.com/thomaswmorris/maria-data/raw/master/maps/einstein.h5: 100%|██████████| 931k/931k [00:00<00:00, 129MB/s]
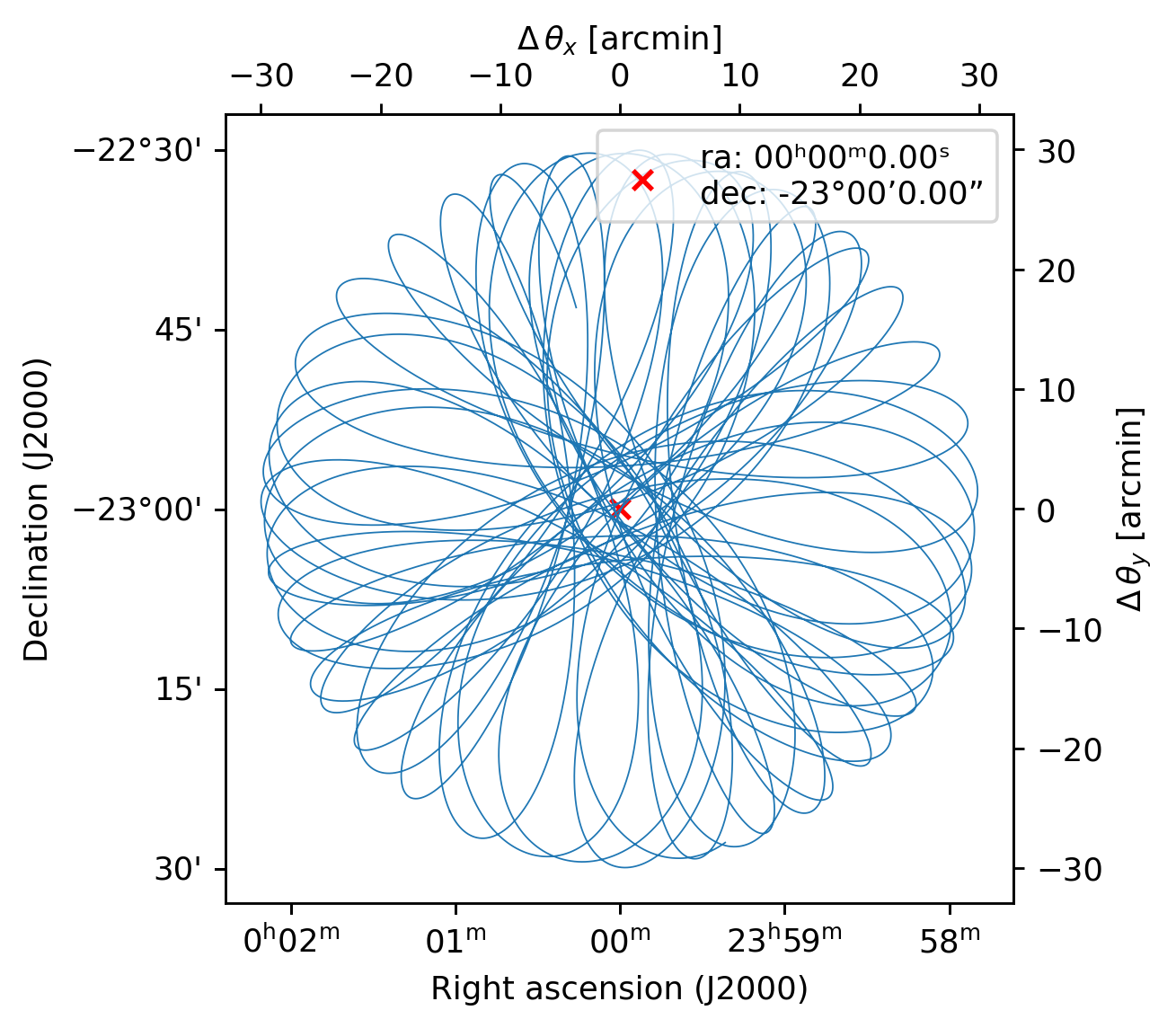
[4]:
from maria import Planner
planner = Planner(target=input_map, site="llano_de_chajnantor", el_bounds=(60, 90))
plan = planner.generate_plan(total_duration=900, # in seconds
sample_rate=50) # in Hz
plan.plot()
print(plan)
Plan:
duration: 900 s
start: 2025-07-13 06:57:22.436 +00:00
end: 2025-07-13 07:12:22.436 +00:00
location:
lat: 23°01’45.84” S
lon: 67°45’17.28” W
alt: 5064 m
sample_rate: 50 Hz
center:
ra: 00ʰ00ᵐ0.00ˢ
dec: -23°00’0.00”
az(mean): 95.71°
el(mean): 62.01°
scan_pattern: daisy
scan_radius: 0.9989°
scan_kwargs: {'radius': np.float64(0.5)}
[5]:
sim = maria.Simulation(
instrument,
plan=plan,
site="llano_de_chajnantor",
atmosphere="2d",
atmosphere_kwargs={"weather": {"pwv": 0.5}},
map=input_map
)
print(sim)
Constructing atmosphere: 100%|██████████| 10/10 [00:33<00:00, 3.39s/it]
Simulation
├ Instrument(1 array)
│ ├ arrays:
│ │ n FOV baseline bands polarized
│ │ array1 652 28.68’ 0 m [f090,f150] True
│ │
│ └ bands:
│ name center width η NEP NET_RJ NET_CMB FWHM
│ 0 f090 90 GHz 20 GHz 0.5 5.445 aW√s 40 uK√s 49.13 uK√s 1.458’
│ 1 f150 150 GHz 30 GHz 0.5 12.25 aW√s 60 uK√s 104 uK√s 0.8748’
├ Site:
│ region: chajnantor
│ location:
│ lat: 23°01’45.84” S
│ lon: 67°45’17.28” W
│ alt: 5064 m
│ seasonal: True
│ diurnal: True
├ Plan:
│ duration: 900 s
│ start: 2025-07-13 06:57:22.436 +00:00
│ end: 2025-07-13 07:12:22.436 +00:00
│ location:
│ lat: 23°01’45.84” S
│ lon: 67°45’17.28” W
│ alt: 5064 m
│ sample_rate: 50 Hz
│ center:
│ ra: 00ʰ00ᵐ0.00ˢ
│ dec: -23°00’0.00”
│ az(mean): 95.71°
│ el(mean): 62.01°
│ scan_pattern: daisy
│ scan_radius: 0.9989°
│ scan_kwargs: {'radius': np.float64(0.5)}
├ Atmosphere(10 processes with 10 layers):
│ ├ spectrum:
│ │ region: chajnantor
│ └ weather:
│ region: chajnantor
│ altitude: 5064 m
│ time: Jul 13 03:04:52 -04:00
│ pwv[mean, rms]: (0.5 mm, 15 um)
└ ProjectedMap:
shape(stokes, nu, y, x): (4, 1, 685, 685)
stokes: IQUV
nu: [90.] GHz
t: naive
z: naive
quantity: rayleigh_jeans_temperature
units: K_RJ
min: -1.000e-02
max: 2.540e-01
center:
ra: 00ʰ00ᵐ0.00ˢ
dec: -23°00’0.00”
size(y, x): (1°, 1°)
resolution(y, x): (5.255”, 5.255”)
beam(maj, min, rot): (0°, 0°, 0°)
memory: 30.03 MB
[6]:
tod = sim.run()
print(tod)
tod.plot()
Generating turbulence: 100%|██████████| 10/10 [00:00<00:00, 11.89it/s]
Sampling turbulence: 100%|██████████| 10/10 [00:07<00:00, 1.29it/s]
Computing atmospheric emission: 100%|██████████| 2/2 [00:05<00:00, 2.70s/it, band=f150]
Sampling map: 100%|██████████| 2/2 [00:10<00:00, 5.06s/it, channel=(0 Hz, inf Hz)]
Generating noise: 100%|██████████| 2/2 [00:01<00:00, 1.74it/s, band=f150]
TOD(shape=(652, 45000), fields=['atmosphere', 'map', 'noise'], units='K_RJ', start=2025-07-13 07:12:22.415 +00:00, duration=900.0s, sample_rate=50.0Hz, metadata={'atmosphere': True, 'sim_time': <Arrow [2025-07-12T17:58:36.259262+00:00]>, 'altitude': 5064.0, 'region': 'chajnantor', 'pwv': 0.5, 'base_temperature': 271.561})
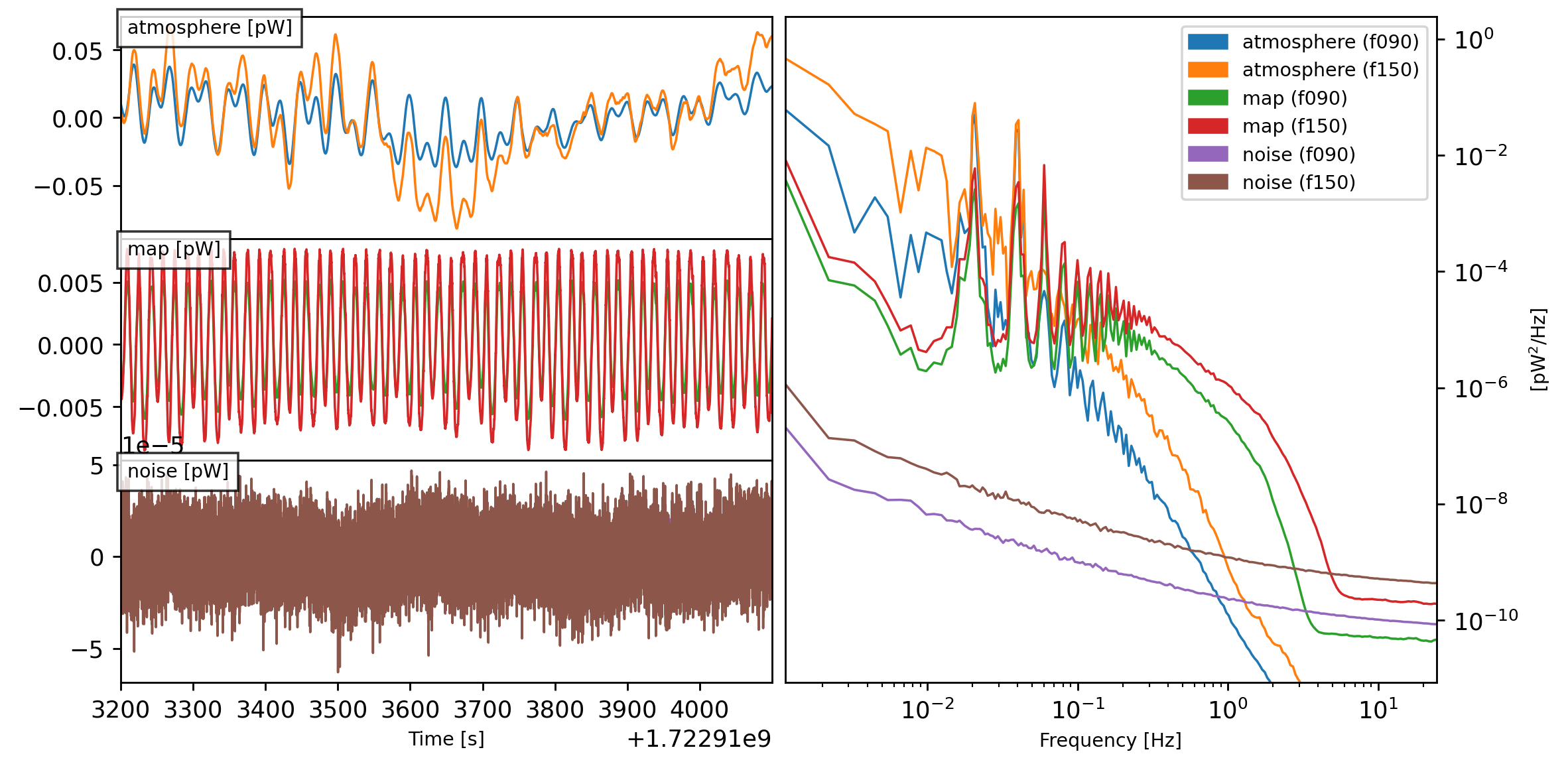
[7]:
from maria.mappers import BinMapper
mapper = BinMapper(
center=(0, -23),
stokes="IQU",
frame="ra_dec",
width=1.0,
height=1.0,
resolution=1.0 / 256,
tod_preprocessing={
"window": {"name": "tukey", "kwargs": {"alpha": 0.1}},
"remove_spline": {"knot_spacing": 30, "remove_el_gradient": True},
"remove_modes": {"modes_to_remove": [0]},
},
map_postprocessing={
"gaussian_filter": {"sigma": 1},
# "median_filter": {"size": 1},
},
units="mK_RJ",
)
mapper.add_tods(tod)
output_map = mapper.run()
print(output_map)
Mapping band f090: 100%|██████████| 3/3 [00:00<00:00, 7.35it/s, band=f090, stokes=U]
2025-07-12 17:59:03.542 INFO: Ran mapper for band f090 in 4.502 s.
Mapping band f150: 100%|██████████| 3/3 [00:00<00:00, 7.37it/s, band=f150, stokes=U]
2025-07-12 17:59:08.015 INFO: Ran mapper for band f150 in 4.47 s.
ProjectedMap:
shape(stokes, nu, y, x): (3, 2, 256, 256)
stokes: IQU
nu: [ 90. 150.] GHz
t: naive
z: naive
quantity: rayleigh_jeans_temperature
units: mK_RJ
min: -2.867e+02
max: 2.107e+02
center:
ra: 00ʰ00ᵐ0.00ˢ
dec: -23°00’0.00”
size(y, x): (1°, 1°)
resolution(y, x): (14.06”, 14.06”)
beam(maj, min, rot): (0°, 0°, 0°)
memory: 6.291 MB
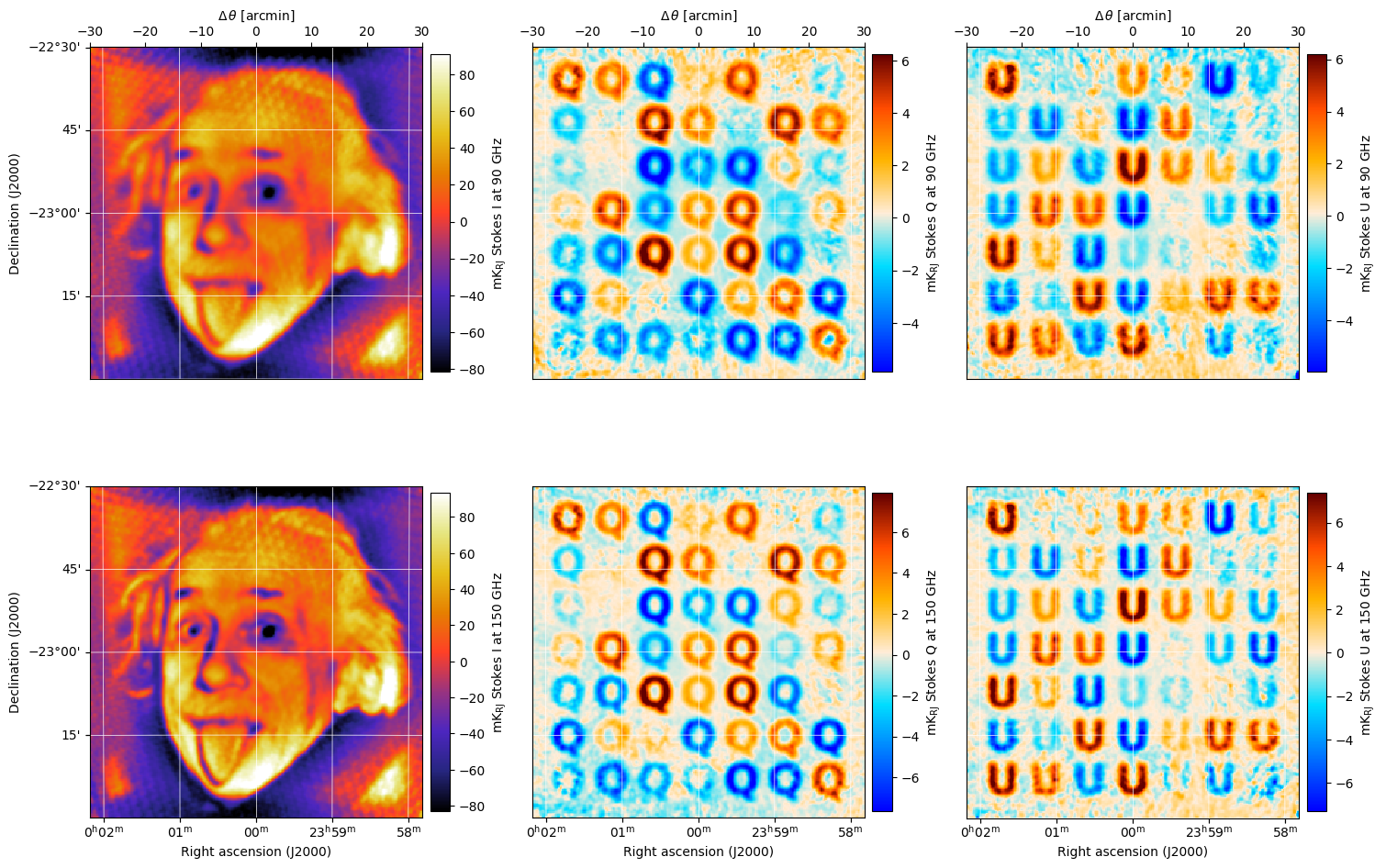
Note that we can’t see any of the circular polarization, since our instrument isn’t sensitive to it.
[8]:
output_map.plot(stokes=["I", "Q", "U"], nu_index=[[0], [1]])
